Analaysis of NORDRAD paired-radar comparison images produced by NRDTOOLS software.

1.Some general observations

• if both radars collect data at the same angle, then the intersection of the two data collection surfaces will lie along a curve that when projected to the earth's surface is a line perpendicular to the join of the radars, and lying half way between them
• if the radars with the same collection angles have the same calibration at all reflectivity values, then the zero difference line will lie on the above-mentioned projected line.
• if the collection angles are the same, but there is a constant calibration difference at all reflectivity values, then the difference value on the intersection line will indicate the calibration difference.
• a constant calibration difference at all reflectivity values will affect all difference values equally, i.e. the image structure will look the same but the colours will have "slipped" on the scale by the calibration difference amount.
• 
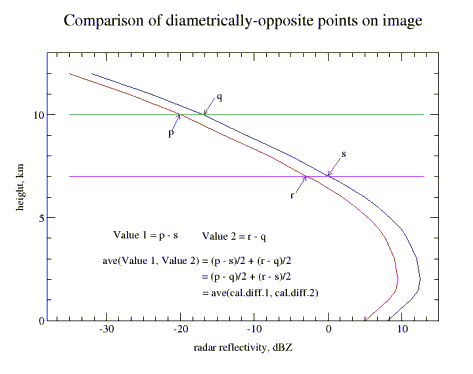
  Fig. 1
  
• if the radars collect at the same angles, the calibrations are identical and the rainfall during the period is distributed uniformly over the area, then the difference image is symmetrical about the join line, and mirror-symmetrical about the perpendicular dividing line, with equal positive and negative values on either side. A difference in calibration will show up as unequal positive and negative values. The average of these gives the average calibration difference (Fig. 1).
• if the radars collect data at different angles, then the intersection curve (which may stop at some point) when projected on the earth's surface will no longer be a straight line but a curve, concave towards the radar with the higher collection angle. For collection angles of 0.5 and 0.6 degrees, the intersection point moves 19 km at a perpendicular distance of 240 km, and 3.5 km on the join (Fig. 2).
• 
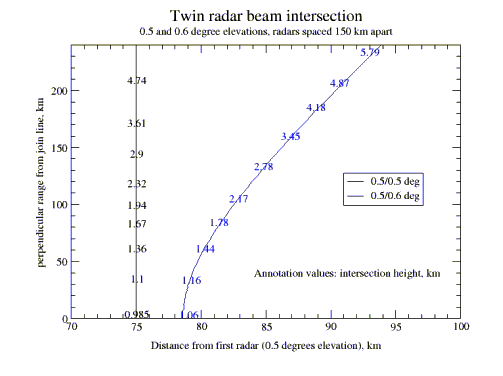
  Fig. 2
  
• The projection of the intersection line as calculated by the NORDRAD software is available from any data file for the area containing a composite of the two radars, and this intersection data can be extracted by the NRDTools software and added to the comparison image. This is highly recommended. A check should be made that the angles used by the NORDRAD software actually correspond with those in use at the radars.
• Another consequence of the two radars collecting at different angles is that the whole image is no longer mirrored about the midpoint line, but is unsymmetrical. The simplest situation is found over the two CAPPI areas of the pseudo-CAPPI (if this is the data form used). In these areas the comparison value at the lower height is from a fixed height, so that the equivalent mirrored points are found from curves representing the same beam height from each radar. For elevation angles of 0.5 - 0.6 degrees, the 0.5 km CAPPI limits lie near 40 km. For radars 150 km apart, the 0.6 deg beam is at a height of about 1.9 km at the edge of the other radar's CAPPI area (at range 110 km). The equivalent range for the lower beam (0.5 degrees) is about 118.5 km. Points at this range lying over the other radar's CAPPI area are thus comparable with the point on the join of the radars at a range of 40 km. Other similar comparison lines can be calculated, e.g. ranges on a radius of 130 km from the 0.6 deg radar are equivalent to those at a range of about 139 km from the radar with the lower beam (over each other's CAPPI areas). Over the remainder of the image the relationships between the pairs of comparable points on each side of the equidistant line are more complex , and must be calculated. There are no lines defined by equal heights of both upper and lower beams on each side of the equidistant line, only point-pairs that are situated (in general) at different distances from the line.
• Due to the non-uniformity of the cumulative rainfall over the image area, the image will in general be neither axisymmetric nor mirror-symmetric. Problems due to this can best be understood by concurrently referring to the single radar cumulative images for the pair of radars. The amount and type of rainfall accumulated must be sufficiently long to produce relatively uniform single- radar accumulations. Experience suggests that the length of a suitable collection period is of the order of two to three weeks.
• Pair comparison data should always be produced using the "and" switch, i.e. a valid echo from both radars is required for a point to be counted. In producing the image it is essential to be able to differentiate between areas having no valid points and those having a difference of zero dBZ. It is suggested that each class should be equally wide, i.e. cover an equal number of bits on the scale. The usable alternatives are thus 1 bit (i.e. each dBZ difference has its own colour, but occupancy may fall too low for meaningful images to be produced; the number of colours needed is also high), 2 bits (which makes the scale unsymmetrical about 0, but is otherwise ok) or 3 bits (which can then be symmetrical about 0, which codes -1, 0 and +1; usually occupancy is more than adequate). With equal-width classes the images better show calibration differences, which produce an equal bias over the whole image.
• The structure of the image is dictated to a very large extent by the form of the average radar reflectivity (vertical) profile, and in particular its vertical gradient, rather than the absolute magnitude of its values. This in turn is very dependent on the time of year. In winter, with very low zero degree isotherm levels and precipitation-forming mechanisms relying upon modest vertical upcurrents, the form of the profile is almost always one in which values monotonically decrease with height. In summer the situation is quite different: the zero degree isotherm is elevated to heights of 2 - 3 km; there is a prevalance of convective-type precipitation mechanisms, which may take larger hydrometeors to considerable heights; lower levels of the atmosphere are drier, allowing the evaporation of descending precipitation. These factors tend to produce average reflectivity profiles that have a maximum well above ground level, a more uniform middle portion and a more rapidly-decreasing upper portion. The consequences of these differences will next be considered.
• Winter situation: the rather uniform gradient at all heights produces neat-looking comparison images that are relatively easy to analyse. Occupancy of the difference classes is high and the overall range of differences is limited. This allows a narrower class range (1 or 2 bits) to be employed, and/or shorter accumulation periods.
• Summer situation: the "nose" in the profile means that the upper beam has no longer automatically smaller dBZ-values than the lower: in certain areas of the image "reverse" areas may appear. If the accumulation is uniform and the collection angles equal, these areas appear nicely mirrored about the equidistance line. Only in areas where upper levels are compared (i.e. where substantial vertical gradients in the reflectivity profile exist) are clearly defined areas found; elsewhere the areas are grainy and poorly defined. Wider difference classes and longer accumulation periods are called for to produce useable data. The best areas of the image for visual analysis are those near the peaks of the ogee and along the nearby outer edges of the image.
• Comprehension of the data images is made easier if an average reflectivity profile for the period is available. This should be possible if vvp-data for the radars concerned is being regularly recorded.
• Comparison between radars having precipitation attenuation compensation and those without this (i.e. at present between Swedish and Finnish radars, respectively) is more complicated than outlined above. Particularly at longer ranges the differences may be quite noticeable, and it is initially better to compare values at shorter ranges. When the main analysis for calibration bias and collection angle difference has been made, this third factor can perhaps be isolated due to its increasing effect with range.
• In principle, radars having a vertical height separation will also produce data that reflects this. This should be taken account of in a properly-structured automatic analysis routine.
• It is standard (and lazy!) practice to speak of a calibration bias or difference between two radars. It should always be remembered that the real situation is one of two different system responses, of which a measurable part is the receiver responses (i.e. the calibration of output voltage against input power). Response curves having differing slopes will then have different "calibration biasses at different signal powers. This may be possible to sift from the comparison data by sorting results by intensity.

2.Procedures for analysis of paired difference images.

• the amount of information contained in a single image is considerable,
• the number of pairs available in the Nordic network is large and
• the complete network analysis and comparison should be carried out at every available opportunity, perhaps 20 times a year.

The automatised approach can take at least one of the following paths:

• a simulation of the manual approach outlined below, in which matched pairs of points are compared (see Fig. 1), or
• a true inverse model approach.

While waiting for the writing and testing of the program embodying the first (or second) approach, it may be useful to pursue the manual method to the extent allowed by resources. The usefulness of the manual method lies in its possibility of activating new insights into the part played by the factors enumerated above: the analyst is in direct visual contact with the material. For this reason the manual method, in the state of development which its has reached now (November, 2000), is briefly described.

3.Manual analysis procedure

• the outer boundary of the data area
• the line on which the radars lie, bisecting the data area (1st. approx)
• the line perpendicular to this, joining the ogees of the data area (referred to hereafter as the equidistance line)
• sets of points lying on circles having the radars as their centre: each set represents data points having a common upper observation level, and a stepped lower level (0.5 km interval seems adequate). The point sets start at the maximum observed height of the radar with the lower collection elevation angle, and are continued down to about a 2.5 km upper level.

Such a transparency, whose points are plotted from x,y values generated by a program (corresponding_points.pl) is needed for all elevation pairs near to that used, i.e. for a 0.6/0.6 nominal pair, the following may be required: 0.5/0.6, 0.5/0.7, 0.5/0.8, 0.4/0.8. It is assumed to a first approximation that the results obtained from, say, 0.5/0.7 are very similar to those from 0.6/0.8, though this still has to be demonstrated.

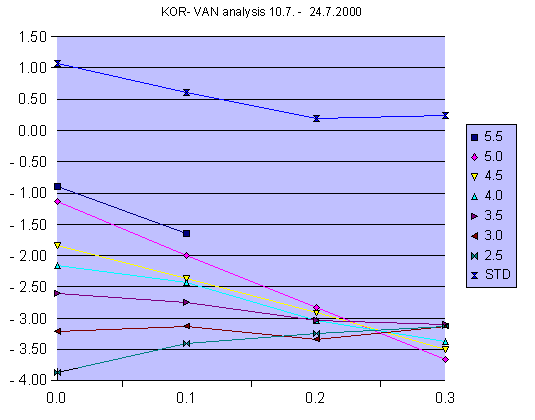
Fig. 3. The abscissa represents the difference in nominal data collection elevation angles, i.e. 0 represents here 0.6/0.6 deg. The y-axis is the average value obtained from each perimeter set: for the upper curve the value is the standard deviation of the perimeter set averages. In this case the calibration bias (difference between radar 1 and radar 2) appears to be approximately -3.2 dB, and the antenna elevation difference about 0.25 degrees, with radar1 below radar2.

The analysis proceeds as follows:

• one template of the set is placed accurately over the colour print-out of the data
• having a hand-portable calculator with statistics facilities to record the values, these are read off the print-out, perimeter by perimeter (the colour key should be at hand for reference). The two points at each ogee of the set should be counted twice.
• after each perimeter set (with a common upper level ) has been read off, its points sum, average and number are recorded in a table (e.g. Excel or equivalent).
• the standard deviation for the average values, as well as the grand total average , are calculated.
• the procedure is repeated for a number of templates, the aim being to find the template sets straddling the values for which the standard deviation of the perimeter averages is a minimum, i.e. that for which the estimate of the calibration bias is the most uniform over the whole data area.
• The values are plotted, as in Fig. 3, and the probable bias and angular error are read from the plot.